TensorBoard Histogram Dashboard
tensorboard中的Histogram面板会展示一些在你的tensorflow graph中随时间发生变化的Tensor的分布。它通过展示在时间轴的不同点上关于你的tensor中许多histograms进行可视化来完成。
一个基本示例
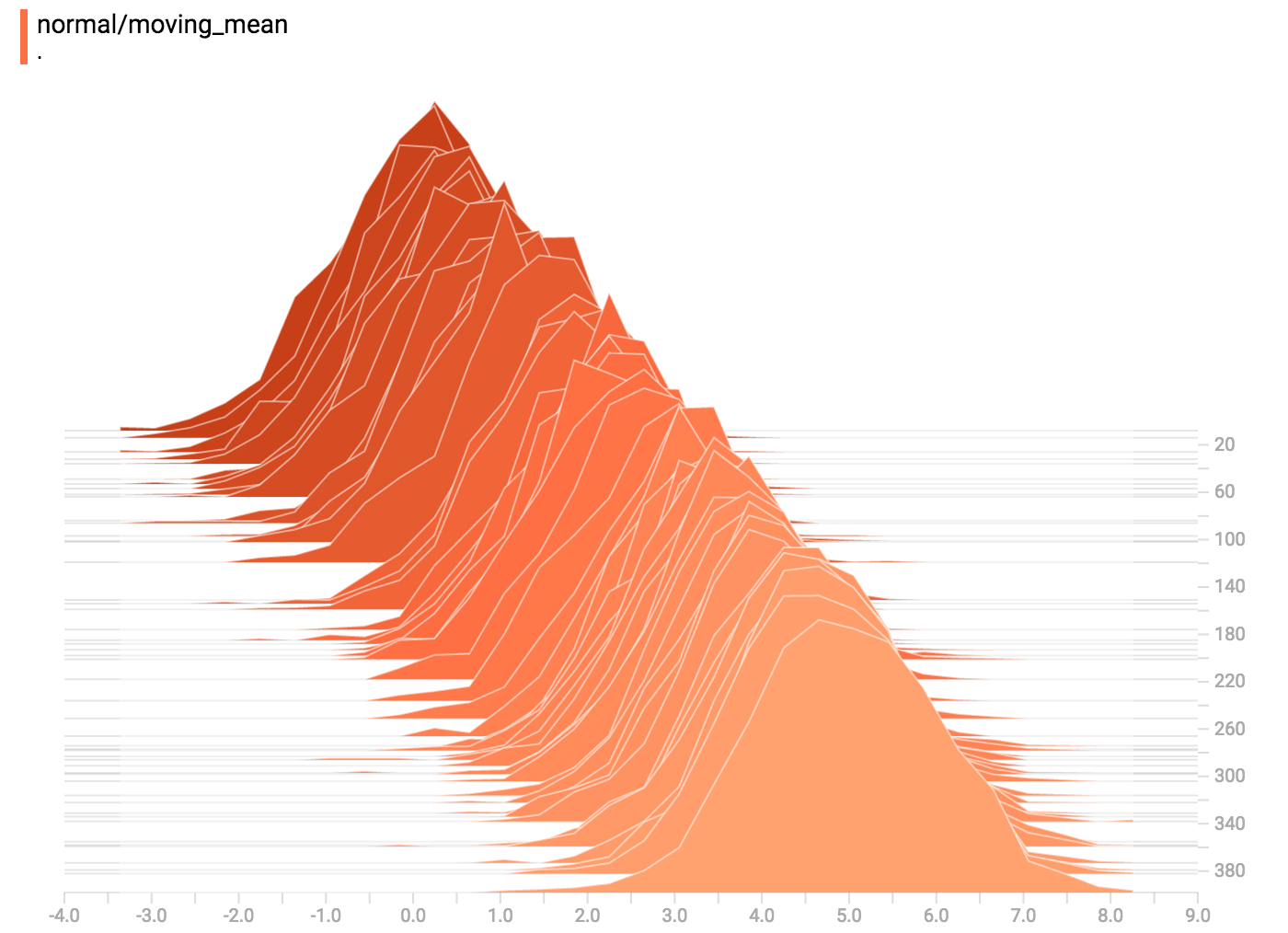
来看个简单示例:一个正态分布变量,它的均值随时间变化。TensorFlow具有一个op:tf.random_normal,它可以用于该示例。通常在TensorBoard中,我们通过使用一个summary op(tf.summary.histogram)来获取数据。关于summary的工作机制,可以参考:TensorBoard教程。
下面的代码段将获取一些histogram summaries,它们包含了正态分布数据,其中分布的均值会随时间增加。
import tensorflow as tf
k = tf.placeholder(tf.float32)
# Make a normal distribution, with a shifting mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# Record that distribution into a histogram summary
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# Setup a session and summary writer
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
summaries = tf.summary.merge_all()
# Setup a loop and write the summaries to disk
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)一旦代码运行,我们通过下面的命令将数据载入到TensorBoard中:
1
tensorboard --logdir=/tmp/histogram_example
一旦TensorBoard运行,可以通过Chrome等浏览器来导航到TensorBoard的Histogram面板。我们可以看到关于我们的正态分布数据的可视化。
tf.summary.histogram采用一个任意大小的size和shape的Tensor,将它压缩成一个histogram数据结构,它包含了许多带有宽度(widths)和次数(counts)的bins。例如:我们希望将数字[0.5, 1.1, 1.3, 2.2, 2.9, 2.99]组织成bins。我们可以做出三个分箱(bins):一个bin包含了从0到1的所有数(包含一个元素: 0.5),一个bin包含了从1到2的所有数(它包含了两个元素:1.1和1.3), 一个bin包含了从2-3的所有数(它包含了三个元素:2.2, 2.9和2.99)
Tensorflow使用相类似的方法来创建bins,但在我们的示例中不一样,它不会创建integer的bins。对于大的、稀疏的数据集,会产生成千上万的bins。作为替代,bins会是指数分布,许多bins接近0, 并且对于非常大的数会产生比较少的bins。然而,可视化指数分布的bins是相当诡异的;如果height被用于编码count,更宽(wider)的bins会占用更多空间,即使它们具有相同数目的元素。相反的,在该区域的编码数(encoding count)会让height的比较变得不可能。作为替代,histograms会将数据进行resample成均匀的bins。这在某些情况下会导致不好的结果。
在histogram可视化上的每个切片(slice)展示了单个histogram。该切片通过step进行组织,较早的切片(older slice,比如:step 0)会进一步“回退(back)”和更暗(darker),其中较新的切片(比如:step 400)会更接近前景色,颜色更亮。右侧的y轴展示了step的数字。
你可以在histogram上移动鼠标来看相应的关于详情的tooltips。例如,在下图中,我们可以看到在第176 step上具有一个中心点位于2.25的bin,它具有177个元素。
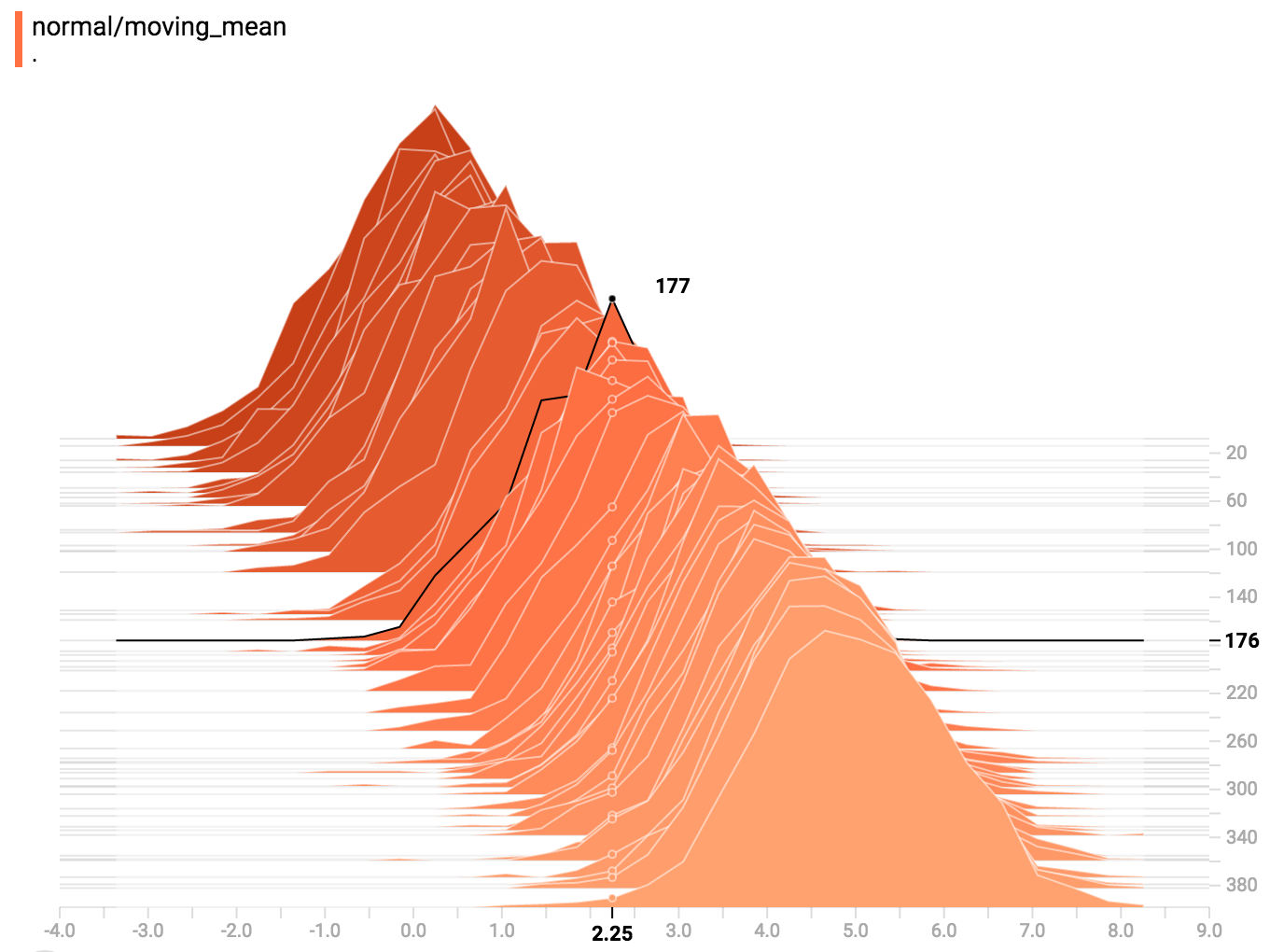
也就是说,你可能注意到,histogram的切片并不总是以step数或时间进行分隔。这是因为TensorBoard使用水塘抽样法(reservoir sampling )来保持关于所有histograms的一个子集,保存到内存中。水塘抽样法(reservoir sampling )可以保证所有样本都具有一个相等的似然,但由于它是一个随机算法,选中的样本不会出现在相同的steps上(even steps)。
覆盖模式(Overlay Mode)
在面板左侧有一个控制部分,它允许你组合选择histogram模式:offset 或者 overlay。
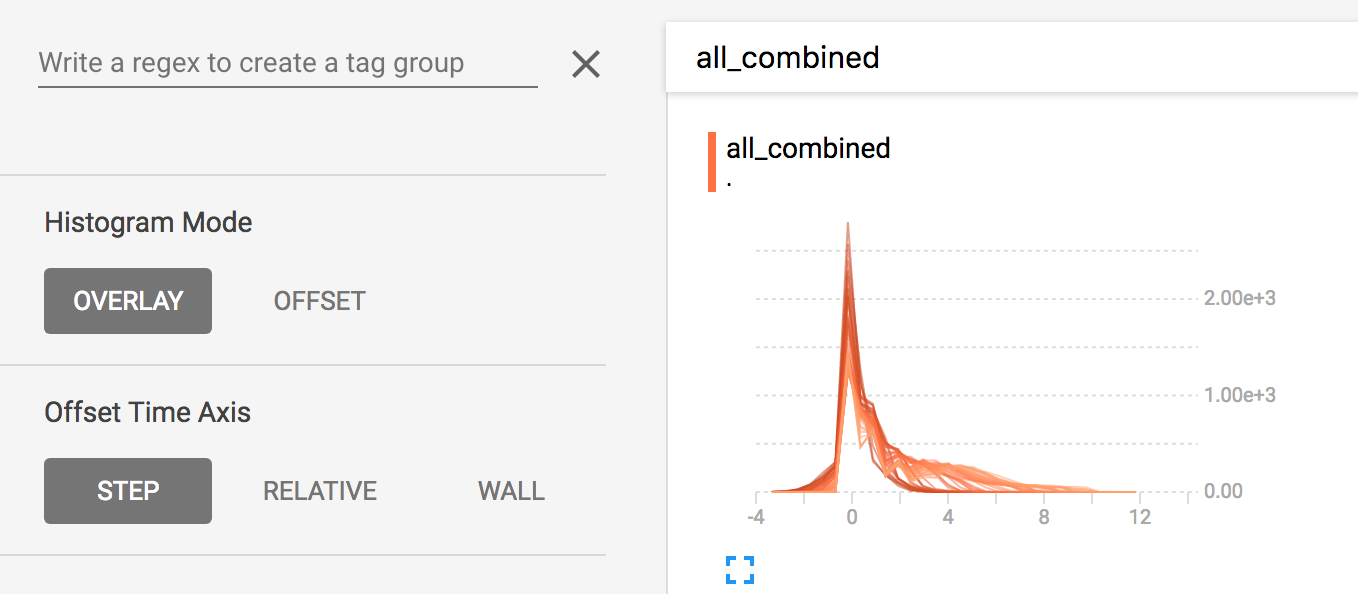
在”offset”模式,可视化会旋转45度,从而每个histogram切片不再在时间上进行展开,相反的,都会打在相同的y轴上。
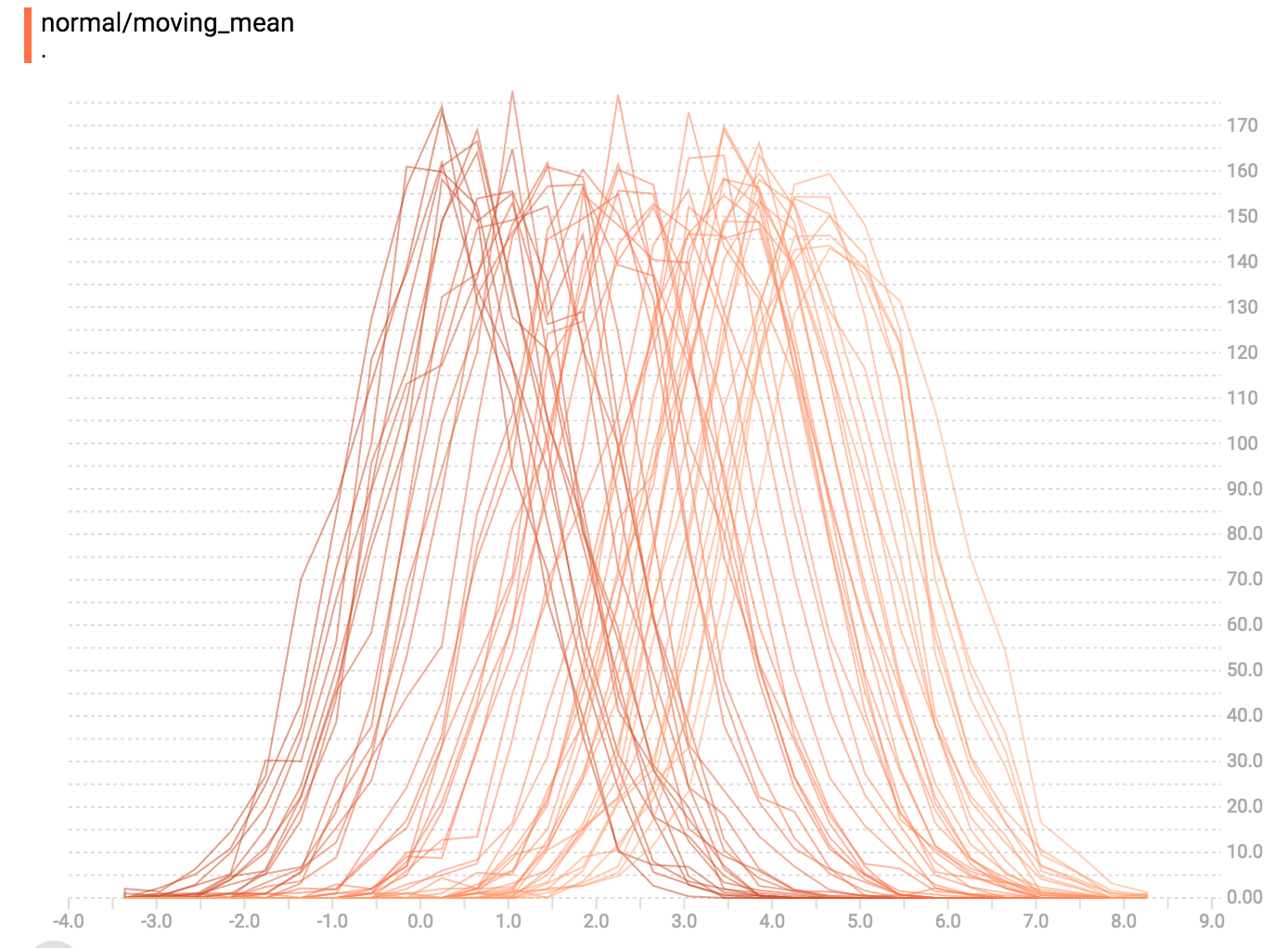
现在,每个slice在图上都是一条独立的线,y轴展示了每个bucket的item count。线越暗表示越早(older,elarlier)的steps,线越亮表示最近最新(recent, later)的steps。你同样可以通过在图上移动鼠标来查看更多信息。
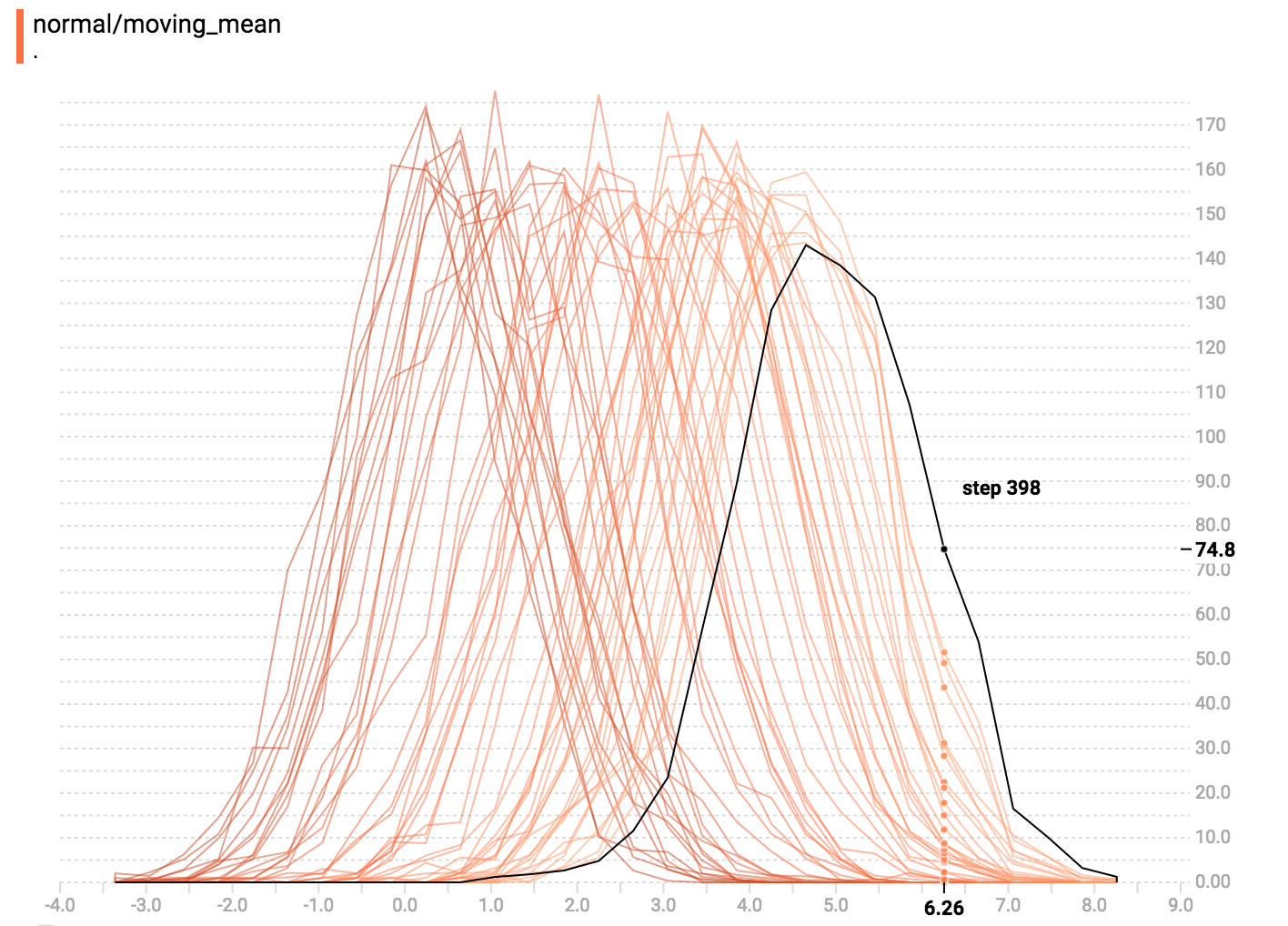
总之,如果你想直接比较不同histograms的counts,使用overlay的可视化会很有用。
多峰分布(Multimodal Distributions)
Histogram面板对于可视化多峰分布(multimodal distributions)很有用。让我们简单构建一个二分分布(bimodal distribution),通过将两个不同的正态分布的输出进行级联得到。代码如下:
import tensorflow as tf
k = tf.placeholder(tf.float32)
# Make a normal distribution, with a shifting mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# Record that distribution into a histogram summary
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# Make a normal distribution with shrinking variance
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# Record that distribution too
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)
# Let's combine both of those distributions into one dataset
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# We add another histogram summary to record the combined distribution
tf.summary.histogram("normal/bimodal", normal_combined)
summaries = tf.summary.merge_all()
# Setup a session and summary writer
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
# Setup a loop and write the summaries to disk
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
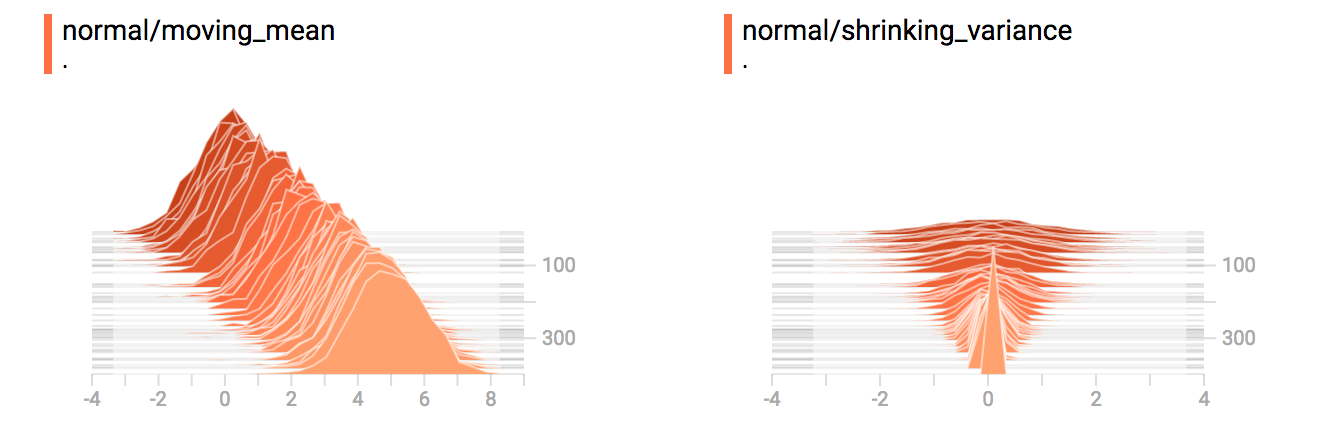
writer.add_summary(summ, global_step=step)你可能还记得我们上例中的“moving mean”正态分布。现在我们也具有一个“shrinking variance”的分布。如图所示:
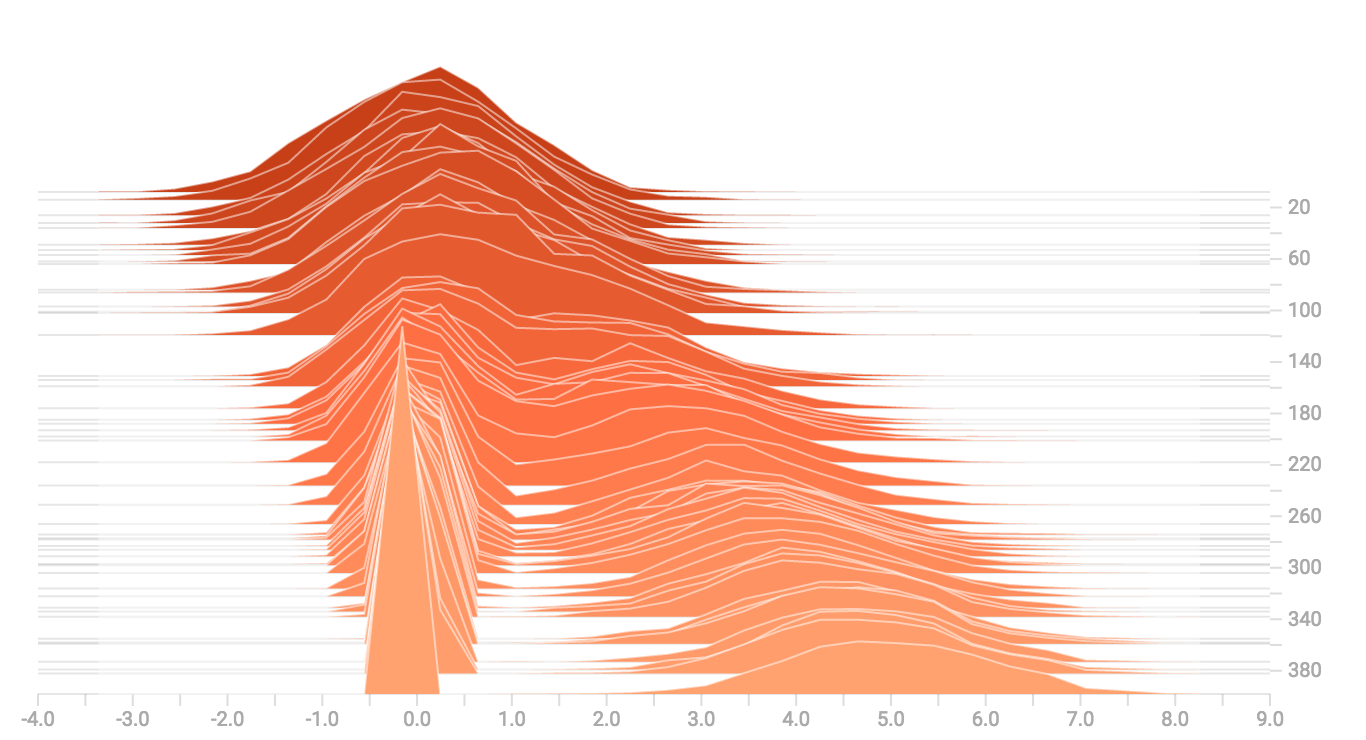
当我们将上面两者进行级联时,我们可以得到一个清楚展示该分叉的二峰结构:
更多分布
我们可以生成和可视化更多的分布,接着将它们合并到一个图中。代码如下:
import tensorflow as tf
k = tf.placeholder(tf.float32)
# Make a normal distribution, with a shifting mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# Record that distribution into a histogram summary
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# Make a normal distribution with shrinking variance
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# Record that distribution too
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)
# Let's combine both of those distributions into one dataset
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# We add another histogram summary to record the combined distribution
tf.summary.histogram("normal/bimodal", normal_combined)
# Add a gamma distribution
gamma = tf.random_gamma(shape=[1000], alpha=k)
tf.summary.histogram("gamma", gamma)
# And a poisson distribution
poisson = tf.random_poisson(shape=[1000], lam=k)
tf.summary.histogram("poisson", poisson)
# And a uniform distribution
uniform = tf.random_uniform(shape=[1000], maxval=k*10)
tf.summary.histogram("uniform", uniform)
# Finally, combine everything together!
all_distributions = [mean_moving_normal, variance_shrinking_normal,
gamma, poisson, uniform]
all_combined = tf.concat(all_distributions, 0)
tf.summary.histogram("all_combined", all_combined)
summaries = tf.summary.merge_all()
# Setup a session and summary writer
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
# Setup a loop and write the summaries to disk
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)Gamma分布
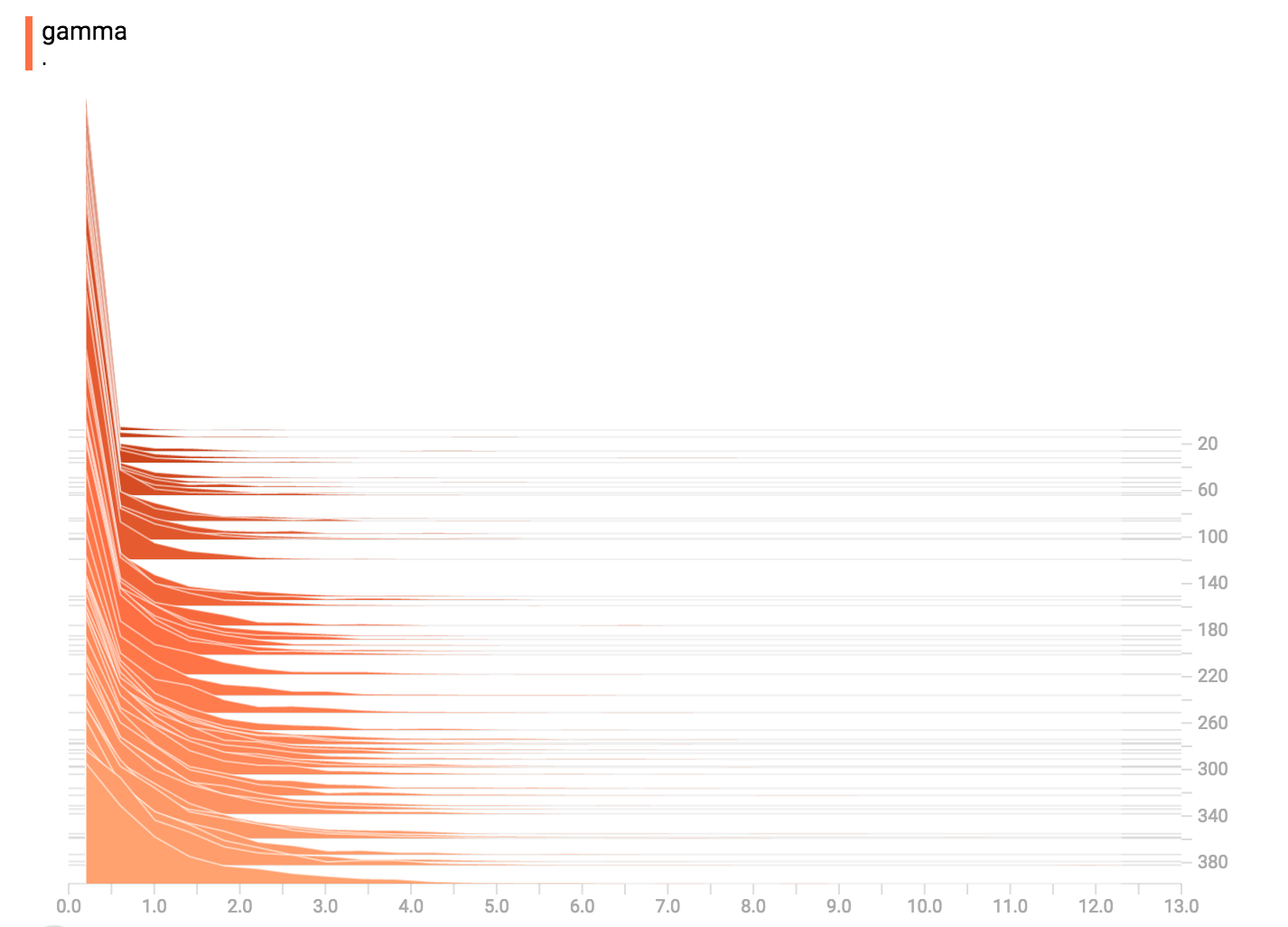
均匀分布
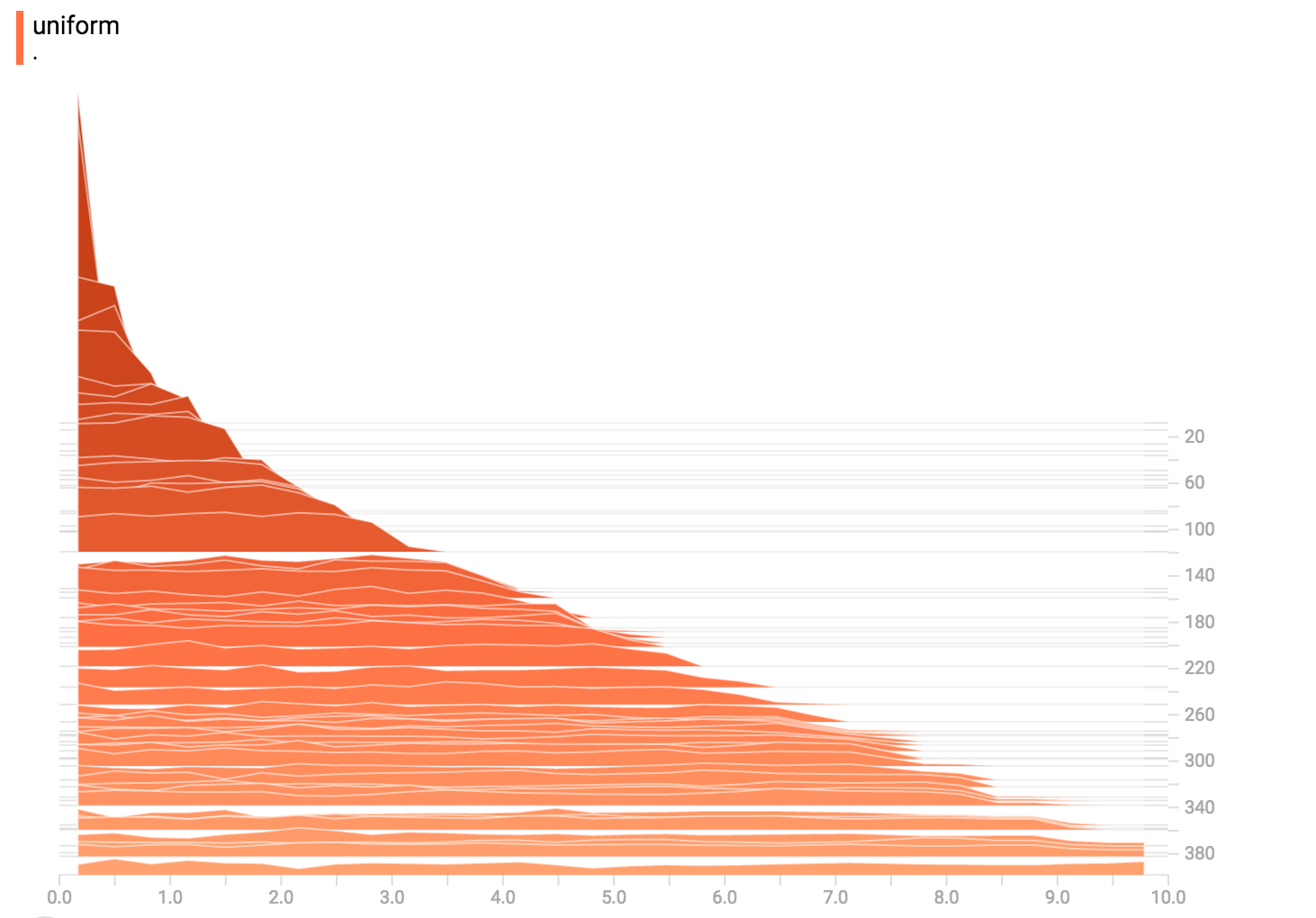
泊松分布
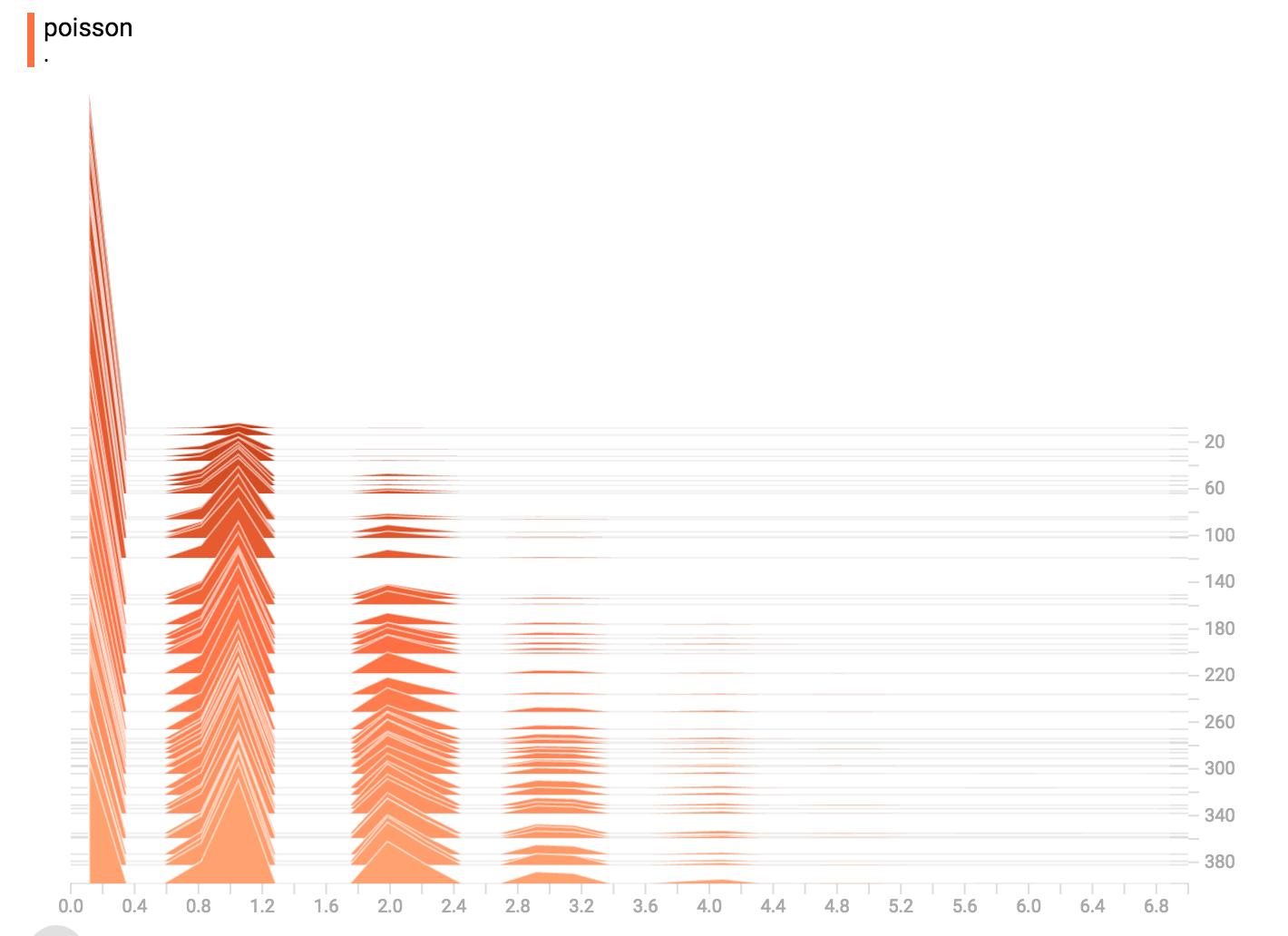
泊松分布被定义在整数上,因而,所有的值被生成为完美的整数。histogram compression将数据移成浮点型的bins,造成该可视化展示了在整数上的碰撞,而非完美的峰值。
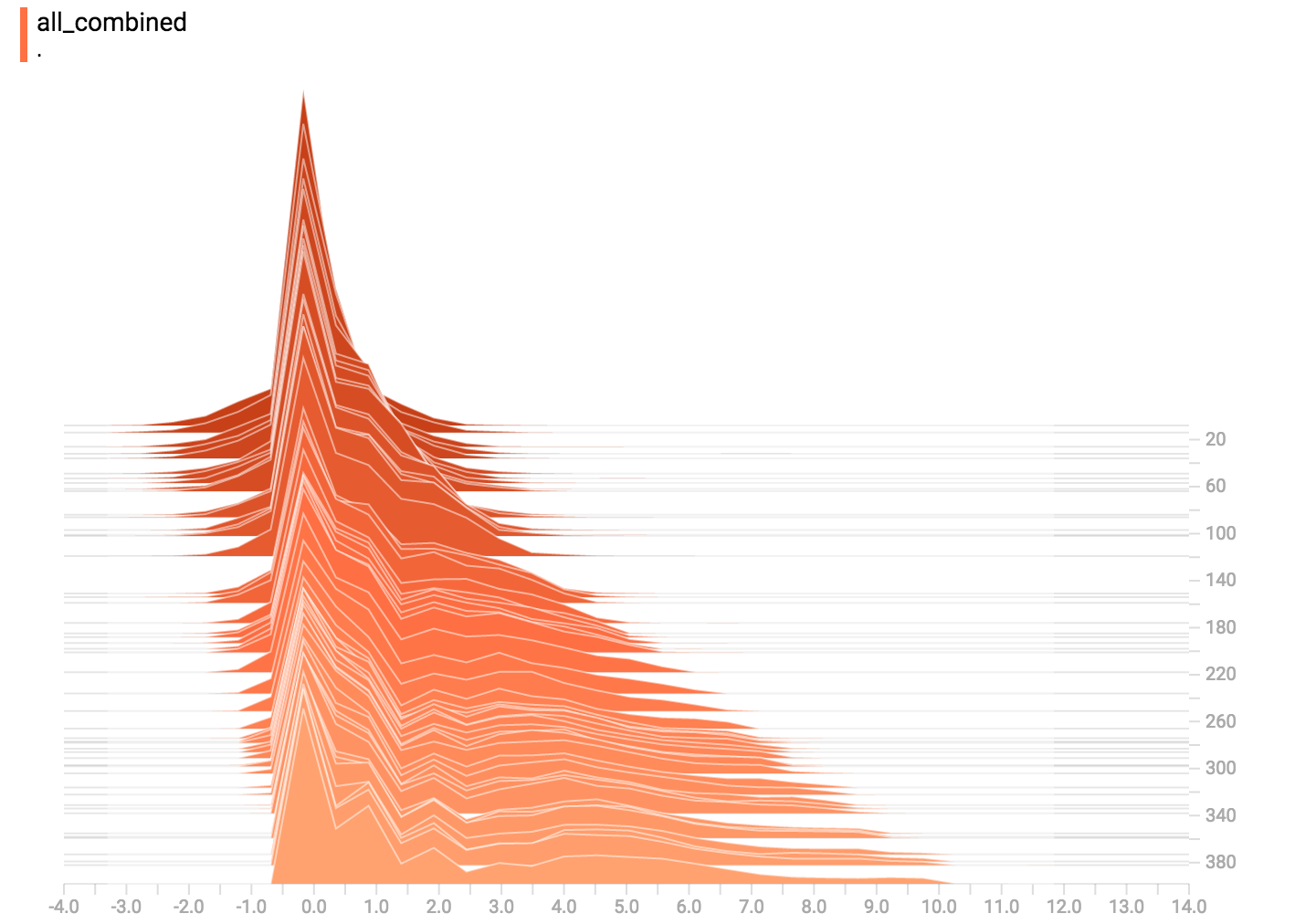
将所有分布合起来
最终,我们将所有数据合起来: